There is a persistent belief among both scientists and non-scientists that good theories must be somehow beautiful or elegant or something similar, because reality itself is ultimately – in some relevant sense – harmonious; or in other words, that science must be beautiful/simple/elegant/etcera because the laws of nature are beautiful/simple/elegant/etcera. This belief is particularly influential in physics and mainstream economics (which likes to mimic physics or an image thereof as much as possible). Sabine Hossenfelder has written an interesting book about how this belief “leads physics astray” rather than that it provides useful guidance.1 For an illustration of how deep the (misguided) belief in “elegance” is rooted in mainstream economics, see the article “Economics as Malignant Make Believe” in this blog. The same belief in beauty/harmony/elegance also influences other scientific fields, however. According to David Orrell, models of climate change are affected by the same bias, for example, leading to more “elegant”, but less accurate models than what would be possible (and necessary).2
Psychology might be able to tell us where this bias comes from, but the question I want to focus on here is what ground there is to believe that reality is – in some relevant sense – “beautiful” or “elegant” or “harmonious” in the first place. An obvious problem is that theses notions in quote marks all seem to be entirely subjective or conventional, but there actually is a case where there might be something like harmony in a more or less objective sense. That case is music. In music, consonance, which is one aspect of harmony (or perhaps, its musical equivalent even), has a physical basis. This doesn’t mean that it is entirely objective what is consonant and what not – in the contrary! – but at least there is some kind of objective ground here. One reason why I find the case of music interesting is that if an aspect of reality in which we can at least make sense of an objective notion of harmony turns out not to be inherently harmonious/elegant/etcetera at all, then what ground do we have to believe that the rest of reality is? (And another reason is that I find music interesting in itself.)
Sound is vibration. The faster air or a string (or something else) vibrates, the higher the pitch. Two different notes sound good together if their vibrations in some sense line up. In that case, they are consonant. If they don’t, they are dissonant. If they are exactly the same pitch, they line up perfectly, of course, but then they aren’t two different notes. If one vibrates exactly twice as fast as the other, they also line up very well. Then the faster vibration sounds exactly one octave higher. If one vibrates exactly three times as fast as the other, or if one vibrates exactly four times in the time the other vibrates three times, then they also line up very well, but the higher these numbers the less consonant the two pitches are. Natural harmonics are the overtones produced naturally in a string or column of air. These are the pitches with two times, three times, four times, etcetera as many vibrations as the fundamental frequency. The other example – that of four vibrations per three vibrations – belongs to a broader class of more or less consonant notes: those with pitch differences that can be expressed as fractions with low numbers as both their numerators and denominators. 3/2, for example, is the perfect 5th, and the previous example of 4/3 is the perfect fourth.
Up to here, things are relatively straightforward, but it becomes considerably less straightforward if we want to somehow measure consonance or dissonance. How much more dissonant is a 23/53 ratio than a 4/3 ratio, for example? And how much more consonant is the 6th natural harmonic than the 31st? We can say that one is objectively more consonant or dissonant than the other – that is, their order is more or less determined by physics and thus in that sense objective – but there is no objective way to put numbers on those consonances and dissonances or to measure those with some kind of objective ruler. But perhaps, we don’t really need to. It would matter if different ways of measurement would lead to fundamentally different results, but it turns out that they don’t.
There are several ways in which one could measure consonance and dissonance. William Sethares suggested the following formula to draw a dissonance curve for a sound \(F\):3
$$D_F(\alpha) = D_F + D_{\alpha F} + \displaystyle\sum_{i=1}^{n}
\displaystyle\sum_{j=1}^{n} d(f_i , \alpha f_j , a_i , a_j ) $$ in which \(f\) are the relevant frequencies (or pitches) and their overtones (i.e. natural harmonics), \(\alpha\) are the “intervals of interest” (i.e. all intervals that are to be included in a graph), \(a\) are the amplitudes (i.e. volumes, more or less) of the various overtones etc., and the function \(d\) is defined as:
$$d(f_1,f_2,a_1,a_2)=a_1a_2[e^{-b_1s(f_2-f_1)}-e^{-b_2s(f_2-f_1)}]$$ wherein \(s\) is defined as:
$$s= {{x^*} \over {s_1f_1+s_2}}$$ This all looks rather complicated, of course, but doing the calculations in a spreadsheet is not that hard (in principle, at least). What isn’t specified by the formulas themselves, however, is how many partials (i.e. the fundamental frequency and its overtones) matter and what their amplitudes should be. Sethares himself suggests 6 with amplitudes 1, 8.8, 7.7, 6.8, 6, and 5.3, but a quick check of some spectrograms of various musical instruments suggests that approximately 10 partials should be taken into account and that their amplitudes can deviate significantly from Sethares’s suggestion. For this reason, my original plan was to calculate, draw, and compare dissonance graphs for various sets of partials and amplitudes at a resolution of 0.1 cent and use that data for further calculations, but that didn’t really work out.
The distance between two semitones (like that between C and C♯) is 100 cents, and thus, an octave spans 1200 cents. To calculate dissonance or consonance at a resolution of 0.1 cent (which seems the minimum necessary to get useful results), the spreadsheet requires 12,000 rows, which isn’t a problem in itself. But for each of these 12,000 rows, there are columns that calculate the interaction between the various partials. The two sigmas in the formula imply that the number of columns is rather large as well if up to 10 partials must be taken into account – namely, 10×10 = 100 plus a number of additional columns – and thus that the total number of cells with calculations is well over 12,000 × 100 = 1.2 million. Although making that spreadsheet wasn’t a problem, anything I tried to append to these calculations made my office software crash, and at some point this corrupted the file. Right now, if I try to open the file, my laptop “thinks” very hard for about 5 minutes (with the fans going berserk to cool down the processor) before the screen turns blue and the computer shuts down.
Fortunately, I copied the results of one calculation to a separate spreadsheet. Those results are the dissonance values based on 10 partials, with an amplitude function that came fairly close to simulating the average spectrogram of a violin, flute, piano, and a couple of other instruments. At least, that’s what I remember, because I cannot open the file to check what the exact amplitude values (and other settings) were. What I do remember is that the reason I saved this particular dataset in a separate file is that I considered them to be the most appropriate measure of dissonance or consonance based on Sethares’s formula. Consonance, by the way, is just 1 minus dissonance (because the values range from 0 to 1). The thick light orange line in the following figure shows the consonance graph based on these values.
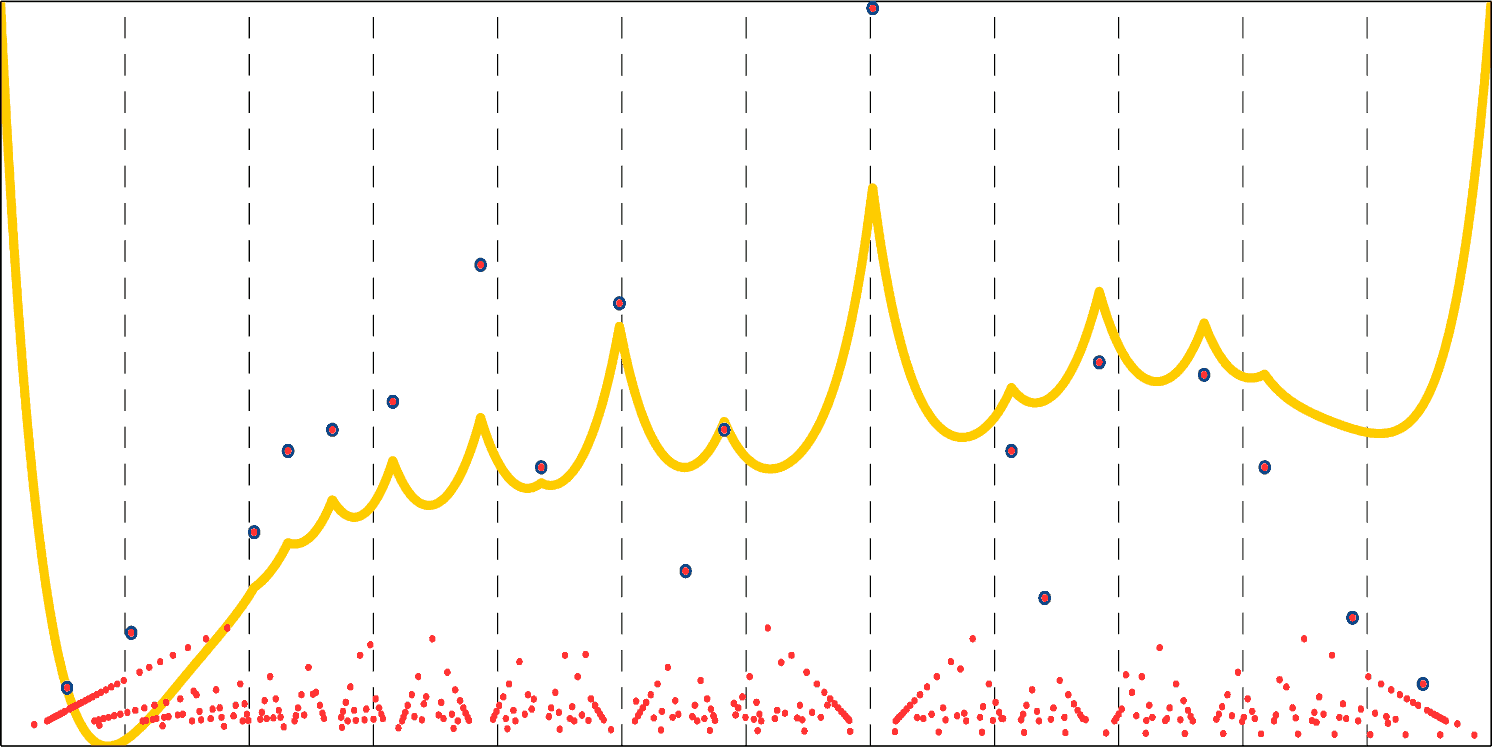This figure obviously also shows a few other things. The x axis ranges from 0 to 1200 cents – that is, one octave. Unsurprisingly, the two most consonant pitches relative to the root note are that same pitch (i.e. a difference of 0 cents) and one octave higher (i.e. a difference of 1200 cents). Those indeed are the peaks in the consonance curve. The next peak is just beyond the 7th vertical dashed line representing 700 cents. That peak is at 702 cents, which is the perfect 5th in just intonation (more about the latter notion below). The red dots represent relatively consonant pitch differences based on the natural harmonic series or low-numbered fractions (see above).4 Their y axis values are the average of the multiplicative inverses of the natural harmonic number or the highest number in the fraction. The red dots with a blue outline, finally, are the red dots that stand out (i.e. have a relatively high y axis value) relative to surrounding dots (on the x axis). These mostly coincide with the peaks in the Sethares-based consonance graph.
What the 19 intervals represented by blue-outlined dots sound like can be heard in the following sound file. The first sound is just the root note (a C); every next sound combines the root note with a note that is exactly as many cents higher as the next blue-outlined dot in the figure. The last, additional sound is one octave (i.e. the first and last sounds are the left and right edges of the figure, respectively). The first and last of the intervals coinciding with the blue-outlined dots are rather dubious – which shouldn’t come as a surprise if you look at the figure – but the rest sound quite consonant to me, and which ones sound better and which sound less good also mostly corresponds with higher or lower y axis values. (I recommend listening to the sound file while looking at the above figure by the way. That way you can easily identify which sound corresponds with which blue-outlined dot.)
The most consonant notes – relative to the root note – are those with the highest y axis values in the above figure. The most consonant, harmonious music is thus the music that includes those notes and no dissonant notes (by the same definition), and the most consonant, harmonious scales includes just consonant notes. Here, things get problematic, however.
Let’s say that you compose a melody in C major where all notes are tuned according to their relative pitches that correspond to the blue-outlined dots (or peaks in the Sethares-based graph) in the figure above. This kind of tuning is called just intonation. At some point, you want to shift your whole melody up by one tone – that is, you want to transpose to D major. Now you have two options: (1) keep the same tuning, but then even a D/A interval – that, is a D with its perfect 5th, which is supposed to sound very consonant – would sound quite awful; or (2) change the tuning of almost every note. In fact, in a just intonation based on D, even the C that you started out with would change, so if you’d transpose to that C next, and retune accordingly, every note would end up 21.5 cents higher than they were in your original C major melody.
Just intonation – a tuning that maximizes consonance for every note in the scale – is relative to the note that you define as the root note. A set of notes that is consonant with C is not the same as a set of notes that is consonant with D, and so forth. There are various other ways of illustrating this and related problems. The “comma pump”, for example, takes a series of repeating notes such as C-G-D-A-E-C with each interval between two notes corresponding to the just intonation interval. In this case too, the second C is 21.5 cents higher than the first, and after nine cycles through the note sequence, C ends up higher than D was in the original sequence.
Perfect harmony in music, then, may be possible as long as you stay in one key and only play chords with the root note of that key as the root note of the chords, but that is extremely limiting. Any deviation requires compromising consonance. Perhaps, this shouldn’t really be surprising – all that the figure above suggests is that consonance is a mess – there is nothing elegant, simple, or beautiful about it.
But can we at least get close? Is there a compromise that addresses the aforementioned problems and that is reasonably close to perfect consonance? The answer is “not really”. We can get fairly close in principle, but any attempt to fix one problem only creates others.
The most obvious first step towards a solution is spreading out notes evenly. The horizontal distance between the blue-outlined dots or the peaks on the curve in the figure above varies considerably. Some are very close together; others are much further apart. It is for that reason that just intonation based on C is almost completely different from just intonation based on D. But if notes would be spread out evenly, then their relative distances are always the same, regardless of what key you’re playing in. This is called equal temperament. An equal temperament solves part of the problem, but only part of it, because it remains a question which equal temperament gets closest to perfect consonance without creating too many other problems.
Equal temperaments really only differ in one respect: the distance between notes. Most equal temperaments divide the octave, but there are other options. Given that an octave interval is most consonant, one might want to preserve that, so dividing the octave is probably the best idea (and not just for that reason). Then, how many notes should there be in an octave? Standard Western music divides the octave into 12 notes. This is called “12EDO” (12 Equal Divisions per Octave), “12ET” (12 Equal Temperament), or “12TET” (12 Tone Equal Temperament). However, that 12EDO is the convention doesn’t imply that it is the best option. It may not be. (And indeed, it probably isn’t, as we’ll see below.) The vertical (dashed) lines in the figure above correspond to the notes of 12EDO. Four of those are very close to blue-outlined dots or peaks in the curve, but the rest is quite far away. And some dots are nowhere near a note in 12EDO (and thus missing altogether). We have gotten quite used to it, so we tend not to notice that both the minor third and the major third (the third and fourth dashed lines) are way off, but if you get yourself accustomed to the pure intervals of just intonation, these two intervals in 12EDO will start to sound horribly out of tune. And that’s what they are. In fact, most of the notes in 12EDO are horribly out of tune – we just don’t notice because we’re used to it. (Which nicely illustrates that what we consider beautiful or harmonious may be determined largely by convention.)
With the data represented by the above figure, it is possible to “measure” whether other equal temperaments do better. “Measure” is in scare quotes here, because there really is no objective way of doing this. There are very many ways that make perfect sense (and many more that don’t), but no objective way of choosing between those. Fortunately, it doesn’t really matter, which (sensible!) calculation method is chosen, because (the relevant aspect of) the results turn out to be nearly identical for all of them.
One obvious way of comparing EDOs is by measuring how far their notes are from the blue-outlined dots in the figure above – that is, from the just-intonated notes. But what should also be taken into account is that the further a note stands out from its neighborhood (i.e. from horizontally nearby red dots) the more margin for error there is. A note can be quite far from the perfect 5th, but still be considered an approximation thereof, but for the first two and last to blue-outlined dots even a 10-cent deviation cannot really be considered an approximation of that note. If this is taken into account, and notes are classified accordingly to how close they get, one ends up with a diagram that looks something like the following:
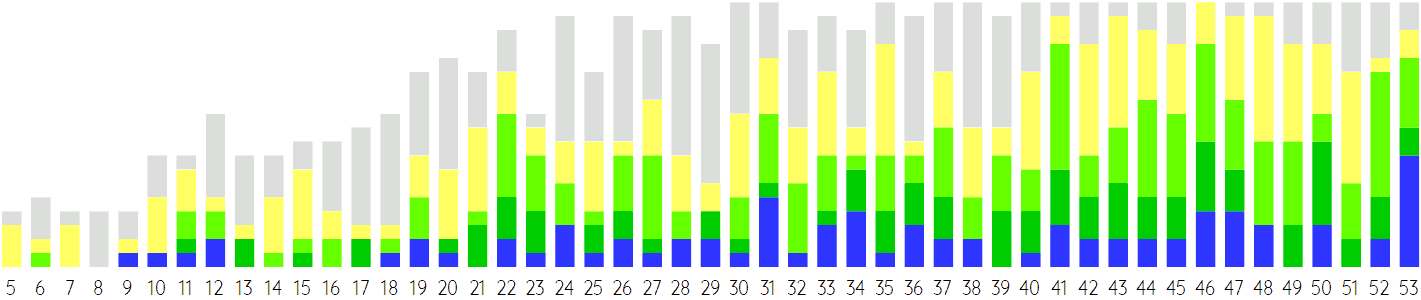In this diagram, blue represents notes that are very close; dark green are good approximations; light green acceptable; yellow bad; and light gray very bad (often so bad that it is quite debatable that it is an approximation of that note at all). If we focus on the green and blue (i.e. “acceptable” or better), then there are very many EDOs that seem much better than 12EDO. 19EDO is the first one that is marginally better; 22EDO seems a lot better, but many of the higher-numbered EDOs – 31, 41, 46, and 53 especially – stand out even more.
There are two further things that need to be taken into account, however. Firstly, not all notes are equally important. Having a good approximation of notes that aren’t that consonant anyway matter much less than having good approximations of the highest peaks in the Sethares-based curve (or of the blue-outlined dots with the highest values on the y axis). Hence, rather than counting notes, they should be weighted by the consonance of their just-intonated counterparts. Or in other words, the higher a blue-outlined dot in the first figure, the higher the weight (i.e. height of bar-segment in the diagram). If the diagram is corrected to take that into account, this is the result:
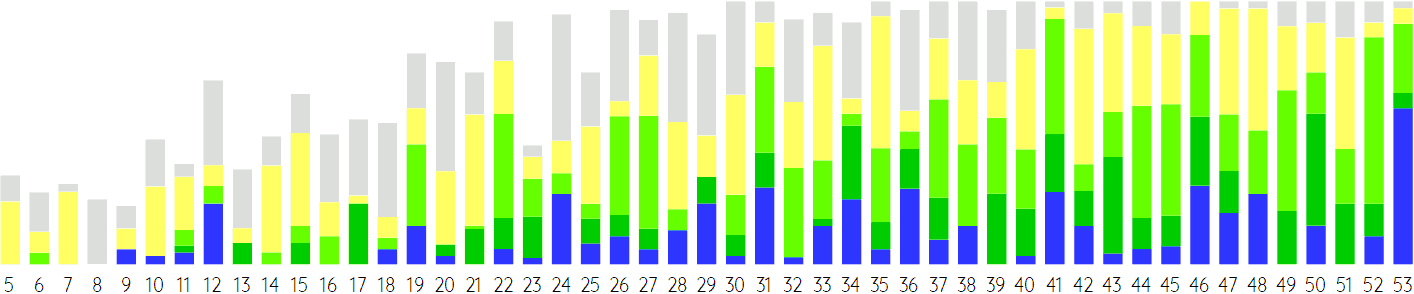Now 12EDO isn’t looking nearly as bad as it did in the first diagram. The reason for that is that 12EDO approximates the perfect 4th and perfect 5th very well – both are off by only 2 cents, which is a difference that we cannot hear anyway (except, perhaps, if you are a trained and experienced piano tuner). And while 19EDO didn’t look very impressive in the first diagram, it suddenly looks a lot better now. (The other way around, 22EDO now looks less impressive.) Most impressive, however, is 53EDO, which already looked good in the first diagram, but which now looks absolutely superb.
But that brings us to the second problem. EDOs with many notes – like 53EDO – are not a solution because they create two other problems. The first of those problems is probably the most obvious: imagine a piano with 53 keys per octave, or a guitar with 53 frets per octave, or a flute with the number of holes, key, and mechanisms needed. Or imagine learning to play the violin (or any other fret-less string instrument) and having to accurately distinguish that many notes. (The learning curve for fret-less string instruments is already steep enough with 12EDO.) Having that many notes per octave might be technically or practically impossible. Doubling the keys on a piano by splitting all of them in half might be doable, but much more than that would be unplayable, or would play so differently that much that is possible on a 12EDO piano is no longer possible. This means that for piano 24EDO might be the upper limit. For guitar, the upper limit is a bit higher than that. 31EDO, which looks pretty good in the diagram, is playable except on a small part of a guitar neck, but the more frets are added, the smaller the part of the neck where one can still comfortably choose the right fret. (Furthermore, the larger the number of frets, the more perfectly they need to be leveled to have a playable instrument.) In case of wind instruments, adding a few more holes is certainly possible, but adding all the extra keys and mechanisms might not. Probably, the upper limit is similar to that of a piano: around 24.
The second reason why equal temperaments with (very) many notes are bad is that they make harmonious modulation (i.e. changing between keys) impossible. In 22EDO, for example, the heptatonic scale in C that approaches the intervals of a just intonated major scale most closely is C-D-E↓-F-G-A↓-B↓ (in what appears to be the most common notation). In 12 EDO, if you’d change keys from C major to D major (as in the example used before) then, you’d add two sharps, and thus, only two notes change (while five stay the same). But if you’d do the same in 22EDO, four notes would change, and only three would remain the same. Hence, while modulating from C major to D major is easy (and not uncommon) in 12 EDO, it is difficult in 22EDO (because the two scales have few notes in common in that EDO). This problem, can be solved easily, however, by adopting the so-called superpythagorean major scale consisting of C-D-E-F-G-A-B (in the same notation). That scale behaves the same as the scale with the same note names (but not the same pitches!) in 12EDO does. But then, instead of getting a better approximation of the major third, for example, you get a far worse one. Actually, now you have a scale that has even worse approximations of all pure intervals than 12EDO, which defeats the very purpose of choosing a larger EDO. And the more notes in your EDO, the bigger this problem: either your scale makes modulation difficult (because approximations of just-intonated scales have few notes in common), or they include many bad approximations of pure intervals. In 31EDO, for example, the only note shared by the C major and D major approximations of just intonation is D, making harmonious modulation all but impossible.
For both technical and musical reasons, then, equal temperaments with more than 24 notes are pretty much useless, which leaves only three contenders: 12EDO, 19EDO, and 22EDO. (And regardless of what method you choose to calculate the consonance of EDOs, this result will stay the same.) Of these three, the third may not be a real contender. Depending on how exactly you measure the consonance of equal temperaments it is slightly better or slightly worse than 19EDO, but in no sensible calculation is it so much better that this justifies the technical problems associated with having that many notes.5 Hence, the main contenders for best equal temperament are 12EDO and 19EDO. Of those two, 19EDO is probably the superior temperament. It approximates many more notes at least acceptably than 12EDO (it has much better 3rds and 6ths, especially, and its 4th and 5th are only slightly worse than those of 12EDO).
This doesn’t mean, by the way, that the other equal temperaments are “bad” or useless. In the contrary, they might be perfect for some purposes. There is death metal in 16EDO and 17EDO, for example, and many other equal temperaments have also been used for a variety of genres (albeit mostly for electronic music).6 The question here, however, is how close we can get to perfect harmony (i.e. to a maximally consonant and musically useful distribution of notes). Aside from 12EDO, 19EDO, and perhaps 22EDO, no other tuning/temperament comes close to satisfying that requirement. Whether 12EDO and 19EDO actually come close is quite debatable, however. 12EDO has only four good notes, and only two of those really matter. 19EDO has a few more, but none of them is (nearly) as close as the good notes in 12EDO. (Of the 8 highest peaks/blue-outlined dots in the first figure, 19EDO approximates 5 fairly closely; 12EDO only 2.) Hence, the conclusion is fairly obvious: no equal temperament can simultaneously approximate a significant subset of important intervals well and be a feasible musical standard.7 But no other kind of tuning system can simultaneously satisfy both requirements either.
Nevertheless, as suggested before, perfectly consonant music is possible if one would adopt just intonation (i.e. a set of intervals corresponding with the peaks/blue-outlined dots in the first figure), but that choice comes with a whole bunch of problems and limitations of its own. Just intonations are specific to the note they are based on and the only chords that are perfectly consonant in a just intonation based on C, for example, are those that have C as their root note. (Furthermore, except in case of fret-less string instruments like the violin, instruments would only be usable in one specific key.) Perfect harmony, then, is possible only in case of drone-like music without key changes and even without significant chord changes. Such perfectly “harmonious” music might not be particularly “beautiful”, “elegant”, or interesting, however, and many people might not even consider it “harmonious”. I wouldn’t be surprised if a survey would show that most people (who are accustomed to Western music) would find Bach fugues, for example, more harmonious, beautiful, elegant, and so forth than such theoretically “perfectly harmonious” music. (And with “not surprised” I mean that that’s the result I’m expecting.) And if that is right, then this shows that even in a case where there is an objective, physical basis to harmony, that objective basis is largely overruled by convention. It’s not nature that determines what is harmonious or beautiful – it’s us.
Why then, should we assume that the rest of reality – where we cannot even make sense of an objective sense of harmony, beauty, or elegance – is harmonious, or that the laws of nature (or “the economy”) are harmonious? In case of sound, harmony really is an ugly, dissonant mess,8 that we try to fit into a usable framework, and on which we project harmony (that is, what sounds harmonious to us largely depends on what we’re used to, even if there is a physical basis). This seems good reason to expect that the rest of reality, which lacks any (obvious) kind of physical analogue to the consonance of sounds, is an even bigger “ugly, dissonant mess”.
There is little reason to believe, then, that the laws of nature are pretty, or simple, or whatever other subjective aesthetic standard we would like to apply. Rather, reality is (probably) “dissonant”, and theories that depict it as harmonious are more likely to be biased idealizations than accurate representations of the real world. What matters for scientific theories is adequacy, coherence, and predictive success (among others). Beauty, harmony, and elegance are not – or should not be – a norm.
If you found this article and/or other articles in this blog useful or valuable, please consider making a small financial contribution to support this blog, 𝐹=𝑚𝑎, and its author. You can find 𝐹=𝑚𝑎’s Patreon page here.
Notes
- Sabine Hossenfelder (2018). Lost in Math: How Beauty Leads Physics Astray (New York: Basic Books).
- David Orrell (2012). Truth or Beauty: Science and the Quest for Order (New Haven: Yale University Press).
- William Sethares (1997). Tuning, Timbre, Spectrum, Scale (London: Springer), pp. 299-300.
- Up till the 127th harmonic and up till fractions with 47 as the highest number, because I had to stop somewhere and adding more didn’t have any discernible effect.
- Except in case of guitars. For those 22EDO is no problem at all.
- My personal favorite, at least right now, is 22EDO, because this temperament both offers a set of reasonably accurate familiar intervals and some new ones not available in 12EDO. To some extent 19EDO does that too, of course, but what 22EDO offers in addition to 12EDO better approximates just intonation than the “extras” of 19EDO.
- Of course, 53EDO satisfies the first requirement, but it doesn’t satisfy the second for reasons explained above.
- Just look at the first figure in this article. How else would you describe that than as an ugly mess?