Longtermism is a variety of utilitarianism (itself a variety of consequentialism) that holds that far-future utility potentially far outweighs near-future utility, and therefore, that we should prioritize far-future consequences of our actions and policies. Utilitarianism is often summarized with the slogan “the greatest happiness for the greatest number of people”, but the term “utility” or “benefits” tends to be preferred by some philosophers (especially those who are close to, or have a background in economics). An associated, even shorter characterization of utilitarianism is that it aims to maximize utility (or benefits). Longtermism, then, holds that we should aim to maximize utility in the far future.
(This article makes extensive use of formalization. The reason for that is that formalization helps me to make my thoughts more precise and the implications of ideas clearer. There isn’t anything particularly complicated or excessively technical in the formalizations used here, but if you have a strong aversion to anything formal, I recommend you to skip ahead to the section titled “A very short and non-technical summary of the above”.)
Utilitarianism and Longtermism
\(X\) is the set of possible actions, policies, and so forth, and \(x\) is one particular action etc. (i.e., \(x \in X\)). Utilitarianism holds that we are required to select the action/policy from \(X\) that has the greatest utility:
$$
x^* =\arg \bigl( \max_{x \in X} V(x) \bigr) ,
\tag{1}
$$ in which \(x^*\) is that required action or policy, and \(V(x)\) is the utility of \(x\). Longtermism accepts this basic idea, but makes a distinction between near-future and far-future utility, such that total utility is the sum of those two:
$$
V(x)=N(x)+F(x),
$$ in which \(N(x)\) is near-future utility, and \(F(x)\) is far-future utility. If we combine these two equations, we get:
$$
x^* =\arg \bigl( \max_{x \in X} \bigl( N(x)+F(x) \bigr) \bigr).
$$ What defines longtermism, however, is not just this distinction between near- and far-future utility, but the idea that because there is much more far future than near future, or at least, there will be far more people in the far longer far future than in the near future, it is the case that:
$$
\max_{x \in X} F(x) \gg \max_{x \in X} N(x) ,
$$ or in (other) words, the maximum utility in the far future is many times larger than the maximum utility in the near future. And because of that, the contribution of \(N(x)\) to \( \max ( N(x) + F(x) ) \) is negligible in comparison to the contribution of \(F(x)\):
$$
\max_{x \in X} \bigl( N(x)+F(x) \bigr) \approx \max_{x \in X} F(x) ,
$$ and:
$$
\biggl( y = \arg \bigl( \max_{x \in X} F(x) \bigr) \biggr)
\; \leftrightarrow \;
\bigl( x^{*} = y \bigr),
$$ or in other words, if some action/policy has the maximum far-future utility, then that action/policy is the best option (and vice versa). This means, of course, that we should maximize far-future utility and ignore near-future utility, which is the defining claim of longtermism.
Cluelessness and expected utility
In a well-known paper (except, perhaps, among longtermists) titled “Consequentialism and Cluelessness”, James Lenman argued that in the long run, unforeseeable consequences vastly outnumber or outweigh foreseen or expected consequences and thus that it is fundamentally unknowable what the actual consequences of an act would be.1 This problem is usually called the “argument from cluelessness” or the “epistemic objection” and is one among many epistemological and metaphysical problems for consequentialism (and thus, for utilitarianism, which is the paradigmatic variety of consequentialism).2 The most common solution for these problems is so-called “subjective consequentialism”, but that “solution” comes with problems of its own.3 Standard utilitarianism as presented above is (presumed to be) a variety of objective consequentialism.4 According to subjective consequentialism (in its application to the present framework), we should not try to maximize actual utility (because that is unknowable), but expected, foreseen, or foreseeable utility.5 So, instead of (1), we get:
$$
\hat x^* = \arg \biggl(
\max_{x \in X} \bigl(
\hat V(x)
\bigr) \biggr) ,
\tag{2}
$$ wherein the hat symbol ^ stands for “expected”. What the formula says, then, is that the expected best action/policy \(\hat x^*\) is the action/policy that has the highest expected utility, \(\max \hat V(x)\). Of course, this means that we need a reasonable method to estimate expected utility \(\hat V(x)\).
Let’s assume that for every possible action/policy \(x\) in \(X\), there is a set \(S_x\) of mutually exclusive scenarios \(s_{x,1}, s_{x,2}, \dots , s_{x,n}\), where each scenario in that set is itself a set of events and states of affairs \(c_{x,1}, c_{x,2}, \dots , c_{x,n}\) that are expected outcomes/consequences of \(x\). Hence, a scenario is an expected possible future or chain of events that could result from action/policy \(x\). There may be cases with only one scenario, but in most cases, many different possible futures – that is, scenarios – are recognized, even if some of them might be very improbable. In any case, all direct and indirect consequences of \(x\) that are expected and that are expected to have (positive or negative) utility must be in one or more scenarios (namely, in those scenarios that describe the possible futures that those consequences are part of). Consequences have consequences themselves and if those are expected and have (positive or negative) utility, those must be included (possibly in additional scenarios) as well.
The expected utility of a scenario is:
$$
\hat V(s_x) =
\sum_{i=1}^n \hat V(c_{x,i}) \times \hat P(\neg c_{x,i} | \neg x),
\tag{3}
$$ wherein \(\hat P(\neg c_{x,i} | \neg x)\) is the estimated probability within that scenario (independently from the probability of the scenario as a whole) of an outcome/consequence not occurring without the action/policy \(x\). \(\hat P(\neg c_{x,i} | \neg x)\) can be thought of as a measure of the necessity of the action/policy for the outcome, and thus a way of removing things that will happen anyway from the calculation.
The overall expected utility of a specific action/policy \(x\), then, is:
$$
\hat V(x) =
\sum_{i=1}^n \hat V(s_{x,i}) \times \hat P(s_{x,i}) ,
\tag{4}
$$ wherein \(P(s_{x,i})\) is the estimated probability that the scenario as a whole reasonably accurately predicts the main outcomes of \(x\) as well as actual total utility resulting from \(x\) and its (direct and indirect) consequences.
A complication: probability distributions
A major complication is that in both (3) and (4), we’re not really dealing with single utility levels and single probability estimates, but with probability distributions, and consequently, “addition” and “multiplication” is not really a matter of adding and multiplying some numbers, but should involve Monte Carlo simulation or some other appropriate statistical technique. Importantly, this means that the result of (4), \(\hat V(x)\) is not a single number either, but a probability distribution that can be represented as a graph with utility on the x-axis and probability on the y-axis. This makes the choice for the best action/policy according to (2) much more complicated. We cannot just pick the highest number, but must compare two or more probability distributions. (One for each policy/action in the comparison.)
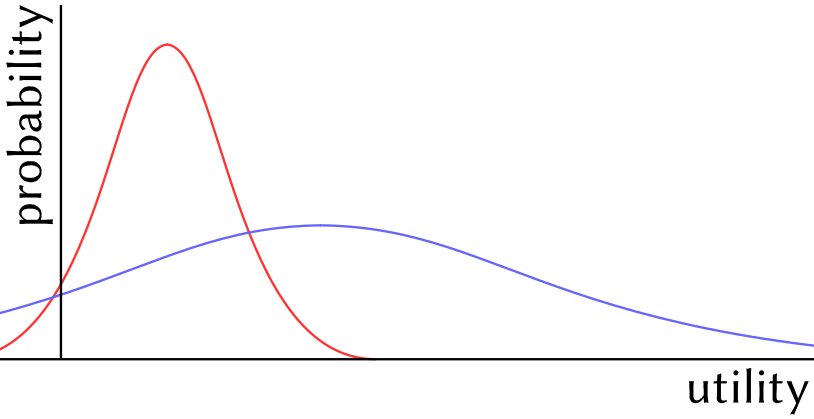 For example, the red and blue curves shown above represent the probability distributions of the expected utility of two different actions/policies. To decide which of these curves – and thus, which of these actions/policies – is better, we need some kind of function or procedure. A function \(\mathfrak{D}\) could be designed to convert these probability distributions into numbers that can then be compared directly:
For example, the red and blue curves shown above represent the probability distributions of the expected utility of two different actions/policies. To decide which of these curves – and thus, which of these actions/policies – is better, we need some kind of function or procedure. A function \(\mathfrak{D}\) could be designed to convert these probability distributions into numbers that can then be compared directly:
$$
\hat x^* = \arg \biggl(
\max_{x \in X} \biggl(
\mathfrak{D} \bigl(
\hat V(x)
\bigr) \biggr) \biggr)
$$ Such a function \(\mathfrak{D}\) should take a number of features of the curve into account: average or median expected utility, which coincides with the peak if a curve is symmetrical as in the example above, but many real probability distributions have fat tails on one end (or even on both), making the average a less useful measure (blue has a higher average and median than red); width/flatness of the curve (blue is wider/flatter than red); the percentage of the surface of the curve that is below zero and thus has negative utility (more for blue than red); the presence of fat tails (which are probably common, but which raise all kinds of difficult questions; there are no fat tails in the figure above), and (possibly?) other relevant aspects of the shape of the curve.
There is no obvious, “objective”, or (presumably) universally acceptable way of designing that function \(\mathfrak{D}\), however. It may even be fundamentally impossible to design a universal function \(\mathfrak{D}\), as the choice which probability distribution is better (or worse) also depends on risk aversion and other psychological characteristics and preferences that differ between cultures and individuals.
While this complication would make the necessary calculations considerably more difficult in real world situations, it is of lesser importance here, so I will ignore the issue and pretend that we can work with single-figure utility estimates.
A very simple example
Let’s assume that we are facing a choice between two options, \(a\) and \(b\). (Thus, \(X=\{a,b\}\)).
policy \(a\) — Invest all available (not yet designated) funds in reducing poverty and preventable diseases.
policy \(b\) — Invest all available (not yet designated) funds in technological means to avoid human extinction.
Let’s further assume that there are four scenarios (two per option) as follows:
| \(s_{a,1}\) | \(s_{a,2}\) | \(s_{b,1}\) | \(s_{b,2}\) | |
| tech innovation and tech jobs | no change | no change | increase | increase |
| poverty and preventable diseases | significant reduction | policy fails (no sig. reduction) | no (significant) change | no (significant) change |
| human extinction (far future) |
yes | yes | no | yes (policy fails or unforeseen cause) |
| \(\hat P(s)\) | high | low | medium | medium |
What is the expected utility of these scenarios? This depends on the expected utility of the various consequence/outcomes (in rows of the table) and their individual utilities, as well as necessities, as defined in (3). The problem is that the expected utilities of most of these outcomes depends largely on further consequences of consequences. The expected utility of technological innovation and tech jobs depends largely on the socioeconomic and other impacts of that innovation and those jobs, for example. And as already mentioned above, those consequences of consequences – in as far as they are expected and have (positive or negative) utility – must be added to the relevant scenarios (which may imply adding scenario variants, which are further scenarios). Furthermore, the expected utility of expected consequences of consequences (of consequences and so forth) may completely change the total expected utility of a scenario. Take scenarios \(s_{b,1}\) and \(s_{b,2}\), for example. In the first, human extinction is avoided, while in the second the attempt to avoid human extinction fails, which may seem to suggest that \(s_{b,1}\) has a much higher utility than \(s_{b,2}\). But what if a further consequence of \(s_{b,1}\) is that humans spread misery throughout the universe (as they arguably have done on Earth), and a further consequence of \(s_{b,2}\) is that more benevolent beings reduce misery throughout the universe? Then that assessment turns around completely. Then \(s_{b,2}\) has much higher utility than \(s_{b,1}\).
Let’s, for the sake of argument, ignore these further consequences (at least for now), and let’s assign some example values to the expected utilities of the various outcomes/consequences in the table. The expected utility of an increase of tech innovation and tech jobs is 1, of a significant reduction of poverty and preventable diseases: 10, of the prevention of human extinction: 1000, and the expected utility of all other (absences of) outcomes is 0. Then, if we assume that \(P(\neg c_{x,i} | \neg x) = 1\) wherever it matters:
$$\hat V(s_{a,1}) = 0 + 10 + 0 = 10,
$$ $$\hat V(s_{a,2}) = 0 + 0 + 0 = 0,
$$ $$\hat V(s_{b,1}) = 1 + 0 + 1000 = 1001,
$$ $$\hat V(s_{b,2}) = 1 + 0 + 0 = 1,
$$ and if we read 80% for high probability, 50% for medium probability, and 20% for low probability, then:
$$\hat V(a) = \hat V(s_{a,1}) \times \hat P (s_{a,1}) + \hat V(s_{a,2}) \times \hat P (s_{a,2}) = 10 \times 0.8 + 0 \times 0.2 = 8,
$$ $$\hat V(b) = \hat V(s_{b,1}) \times \hat P (s_{b,1}) + \hat V(s_{b,2}) \times \hat P (s_{b,2}) = 1001 \times 0.5 + 1 \times 0.5 = 501.
$$ Since 501 is more than 8, we should prefer policy \(b\).
Longtermism separates far-future utility from near-future utility. In a subjective consequentialist framework, we have:
$$
\hat V(x)= \hat N(x) + \hat F(x),
$$ in which \(\hat N(x)\) is expected near-future utility, and \(\hat F(x)\) is expected far-future utility. In the example, the utility of avoiding human extinction is far-future utility, while all other utility is near-future utility. Thus:
$$\hat N(s_{a,1}) = 10 \; , \; \hat F(s_{a,1}) = 0 ,
$$ $$\hat N(s_{a,2}) = 0 \; , \; \hat F(s_{a,2}) = 0 ,
$$ $$\hat N(s_{b,1}) = 1 \; , \; \hat F(s_{b,1}) = 1000 ,
$$ $$\hat N(s_{b,2}) = 1 \; , \; \hat F(s_{b,2}) = 0 .
$$ \(\hat N(\cdot)\) and \(\hat F(\cdot)\) can be calculated by means of (4) if \(\hat N\), respectively, \(\hat F\) is read for \(\hat V\):
$$\hat N(a) = 8,
$$ $$\hat F(a) = 0,
$$ $$\hat N(b) = 1,
$$ $$\hat F(b) = 500.
$$ From these numbers it obviously follows that:
$$\arg \biggl( \max \bigl( \hat N(x) + \hat F(x) \bigr) \biggr) = \arg \biggl( \max \bigl( \hat F(x) \bigr) \biggr),
$$ or in other words, near-future utility is largely irrelevant and the choice between policies \(a\) and \(b\) is entirely determined by far-future utility. Notice that this still would be the case if non-extinct humans would spread misery throughout the universe in the far future. Then, \(\hat F(b)\) would be a very large negative number and we should choose \(a\) instead, but the choice would still be determined by far-future utility.
Uncertainty
In the example in the previous section, it is uncertain what the utility of human extinction (or survival) is. Longtermists typically assume that this utility is humongous because they expect that there are very, very many humans in the far future, but there are reasons to doubt that. First of all, one may wonder whether total utility of all sentient beings on Earth currently is positive. Fading affect bias may make us overestimate the utility of our own lives, leading to an overestimation of the total utility of all sentient life. It is not impossible that due to this effect and other biases and illusions we fail to realize that total utility of sentient life on Earth is actually negative. (Notice that I’m not saying that it is; merely that this is a possibility.) And if that is the case, there is no reason to believe that this would be fundamentally different in the (far) future.
Secondly, it is easy to come up with many more or less plausible scenarios in which human survival (i.e., non-extinction) leads to greater disutility (i.e., negative utility overall). I already mentioned one such scenario above, namely, the scenario in which far-future humans spread misery throughout the universe. This could be their own misery (as humans are quite good at making other humans and themselves miserable), but it could also be the misery of other sentient beings, either intelligent (such as “aliens”, AI, etc.) or non-intelligent (i.e., non-human animals). Notice that utilitarianism typically takes all utility into account, and that any variant that restricts relevant utility to just humans (or humans and their descendants) is guilty of a kind of arbitrary discrimination called speciesism, which is not fundamentally different from racism. (This doesn’t mean that microcellular organisms on some distant planet are as relevant as humans, for example. There are non-arbitrary reasons why it may be the case why the utility of intelligent beings should be prioritized, at least to some extent.)
Anyway, my point here is that the utility of human extinction or survival is uncertain. This could be dealt with in the framework proposed above by positing many different scenarios (with different scenario probabilities) for every possible variant with its various consequences and their utilities. In many cases, it may be preferable to take a shortcut, however, by ignoring all these variant scenarios and adjusting the main scenario (that these variants split off from) by taking uncertainy into account. Towards that end, let’s introduce a new operator \(\text{atr}( \dots )\) that returns the certainty level (between 0 and 1) of whatever goes on the dots. (“atr” comes from Greek ἀτρέκεια, which means “certainty”, among others.) So if \(e\) stands for “Earth will continue on its orbit around the Sun tomorrow” and \(j\) stands for “Jupiter will crash into Earth tomorrow”, then \(\text{atr}( e )\) and \(\text{atr}( j )\) are almost 1 and 0, respectively.
With this new operator, we can adjust (3) as follows:
$$
\hat V(s_x) =
\sum_{i=1}^n \hat V(c_{x,i}) \times \hat P(\neg c_{x,i} | \neg x) \times \text{atr} \bigl( \hat V(c_{x,i}) \bigr).
\tag{5}
$$ If we apply this new formula to the example above, we need to quantify our certainty about the utility of human survival (which was 1000 in the example). I’m inclined to say that this certainty is very low for reasons mentioned above. For argument’s sake let’s say it is 0.1. Then \(\hat V(s_{b,1})\) isn’t 1001 (as above) but 101, and \(\hat V(b)\) is 51. This is still more than the utility of \(a\), which was 8, but the two options are now much closer together.
Cluelessness and expected utility (again)
Now, let’s add cluelessness to the mix. Recall that the point of Lenman’s charge of cluelessness is that in the long run unforeseeable consequences vastly outnumber or outweigh foreseen or expected consequences. Any action or policy has some direct and indirect consequences that can be reasonably foreseen, but there always also are unforeseen consequences, and all those foreseen and unforeseen consequences have further consequences. The more steps away, the larger the share of unforeseen, or even unforeseeable indirect consequences. It doesn’t take many steps before the unforeseeable starts to overwhelm what we can reasonably predict.
Let’s symbolize the set (or mereological sum, as it is quite debatable whether consequences are countable entities) of actual consequences of some action/policy \(x\) as \(A_x\). Recall that scenarios \(s_{x,1}, s_{x,2}, \dots , s_{x,n}\) in \(S_x\) are sets of expected consequences. A scenario can fail in two ways: by predicting consequences that aren’t in \(A_x\) (i.e., don’t/didn’t happen), and by not predicting consequences that are in \(A_x\) and that have significant utility effects. Cluelessness concerns the second failure and implies that in the long run, \(A_x \backslash s_x\) (i.e., non-predicted actual consequences) will have many more members than \(s_x\). This has (at least) two important implications.
First, because \(P(s_{x,i})\) in (4) is the estimated probability that scenario \(s_{x,i}\) reasonably accurately predicts the main outcomes of \(x\) and actual total utility resulting from \(x\), and because in the long run unforeseen (non-predicted) consequences vastly outnumber predicted consequences, for any \(s_{x,i}\), \(P(s_{x,i}) \approx 0\). (This is really just another way of phrasing the main point of cluelessness.) However, this problem can be addressed, at least to some extent, by temporaly restricting sets of consequences, such that \(A_x^F\) is the subset of actual far-future consequences (\(A_x^F \subset A_x\)), \(s_{x,i}^N\) is the subset of near-future consequences in \(s_{x,i}\), and so forth. If we define the “near future” as at most a few decades ahead (or maybe a little bit more in some cases), and the “far future” as everything beyond that, then, because for any near-future scenario \(s_{x,i}^N\) it is the case that:
$$
\sum_{\Large{a \in A_x^N}} | V(a) | > \sum_{\Large{c \in s_{x,i}^N}} | \hat V(c) |,
$$ that is, total absolute actualized utility is larger than total absolute predicted utility,6 it follows that \(P(s_{x,i}^N)\) is small but not likely to be close to zero in most cases. Or in other words, we can make reasonably accurate predictions of near-future utility effects of actions policies, where “reasonably accurate” means that these predictions have non-negligible probabilities.
For any far-future scenario \(s_{x,i}^F\), on the other hand,
$$
\dfrac
{\sum_{\Large{c \in s_{x,i}^F}} | \hat V(c) |}
{\sum_{\Large{a \in A_x^F}} | V(a) |}
\approx 0
$$ (i.e., total absolute predicted utility divided by total absolute actualized utility is approximately zero), meaning that \(P(s_{x,i}^F) \approx 0\).
By extension of (4), expected far-future utility of an action/policy is given by:
$$
\hat F(x) =
\sum_{i=1}^n \hat V(s^F_{x,i}) \times \hat P(s^F_{x,i}) ,
\tag{6}
$$ and given that for every \(s_{x,i}^F\), \(P(s_{x,i}^F) \approx 0\), and that there cannot be enough scenarios to compensate for this, it follows that:
$$ \hat F(x) \approx 0.$$
Furthermore, the larger the temporal distance from the present, the greater the uncertainty with regards to the expected utility of expected outcomes/consequences as well, which is largely due to the exponential increase of further consequences that have further utilities. This can be dealt with either by increasing the number of scenarios, or by decreasing the certainty of utility assessments as suggested in the previous section. In practice, only the second option is available because the number required for the first option would quickly become unmanageable, and then continue to increase exponentially even further into the future. Consequently, in any reasonable and feasible approach to utility estimation, the certainty levels of expected utilities of outcomes are taken into account as formalized in (5). Because, as mentioned, these certainty levels reflect further consequences, and expected further consequences are (due to cluelessness) vastly outweighed/outnumbered by unforeseen/unforeseeable further consequences in the far future, for any consequence \( c_{x,i} \in s^F_x \), \( \text{atr} \bigl( \hat V(c_{x,i}) \bigr) \approx 0 \), that is, certainty about expected utility of expected far-future consequences is approximately zero.
Since this applies to all consequences \( c_{x,i} \in s^F_x \) and no scenario can have enough consequences to compensate for this effect, this implies that for any scenario \(s_{x,i}\), (5) gives \(\hat V(s_{x,i}^F) \approx 0\). Consequently, while it was argued above that cluelessness implies that \(\hat P(s^F_{x,i})\) in (6) is approximately zero, uncertainty implies that \(\hat V(s^F_{x,i})\) is approximately zero as well:
$$
\hat F(x) =
\sum_{i=1}^n
\underbrace{
\hat V(s^F_{x,i})}_{\approx 0}
\times
\underbrace{
\hat P(s^F_{x,i})}_{\approx 0},
$$ which further strengthens the above conclusion that:
$$ \hat F(x) \approx 0.
$$ And therefore, contrary to longtermism,
$$
\max_{x \in X} \hat N(x) > \max_{x \in X} \hat F(x) ,
$$ or in (other) words, maximum expected utility in the near future is larger than maximum expected utility in the far future. And because of that, the contribution of expected far-future utility \(\hat F(x)\) to expected total utility \( \max ( \hat N(x) + \hat F(x) ) \) is negligible in comparison to the contribution of expected near-future utility \(\hat N(x)\):
$$
\max_{x \in X} \bigl( \hat N(x) + \hat F(x) \bigr) \approx \max_{x \in X} \hat N(x) ,
$$ and thus:
$$
\biggl( y = \arg \bigl( \max_{x \in X} \hat N(x) \bigr) \biggr)
\; \leftrightarrow \;
\bigl( \hat x^{*} = y \bigr),
$$ or in other words, if some action/policy has the maximum near-future utility, then that action/policy is the best option (and vice versa), which means that – contra longtermism — we should maximize near-future utility and (mostly) ignore far-future utility.
Well, actually … No, not exactly. To some extent, this conclusion results from the very crude division between the near and far future. If we’d add a “mid future” in between for the time scale of a few decades until a few centuries, then it wouldn’t follow that only the near future matters. The IPCC reports are a good illustration of this. For pretty much every prediction about climate change in those reports, a “confidence” level is mentioned. Those confidence levels often concern the certainty about the occurrence of some consequence, but sometimes also about the seriousness of its effects, which is quite close to its expected (usually negative) utility. From these reports and related data, utilities, probabilities, and certainty levels needed as inputs in (5) can be inferred, and these do not (necessarily) result in zero mid-future utilities. Hence, in addition to the near future, the mid future matters too.
Furthermore, we don’t really need this separation between near- and far- (and mid-) future utility. What matters is things like our confidence (or certainty) about expected consequences and their utilities. With data like that, we an use formulas or procedures like (5) and (4) to decide what to do. Due to cluelessness, the near future will matter more in those decisions, followed by the mid future, while the far future doesn’t really matter at all, but we don’t need to separate consequences and utilities by time (and draw arbitrary boundaries between them) to see that.
A very short and non-technical summary of the above
According to the “argument from cluelessness”, in the long run, unforeseeable consequences vastly outnumber or outweigh foreseen or expected consequences, and therefore, it is fundamentally unknowable what the actual consequences of an act would be. Because of this we cannot decide what to do based upon actual (future) consequences, but only based upon expected consequences. Furthermore, cluelessness is related to temporal distance from the presence. The further in the future our predictions about the consequences of an action or policy, the more clueless we are, or in other words, the less certain we can be about what actually will happen (and what further consequences consequences will have) and what the utility of (actual or predicted) consequences will be. Because of this, our predictions for the far future have a probability close to zero, and our reasonable confidence in predictions about utility should be close to zero as well. Because of this, a reasonable method to assess expected utility of actions or policies results in far-future utilities close to zero, while maximum expected near-future utility tends to be low, but higher than that. This implies in turn that in our calculations to decide the best thing to do, the far future doesn’t really matter, and that it is the near-future consequences and their utility that largely determine our best course of action, which is the very opposite of what longtermists claim.
Why none of the above matters
The set of expected consequences from publishing this article doesn’t include the event of a longtermist changing their mind. The reason for that is that I suspect that, ultimately, the appeal of longtermism is not in the (flawed) argument in its favor, and thus that exposing flaws in that argument doesn’t matter. Rather, the appeal of longtermism to its adherents is in its implications. Longtermism suggests that we should invest more in technology and less in international aid, for example. It suggests that we should forget about the suffering of the disposable masses that won’t make any significant contribution to the future anyway, and instead focus on the people and policies that do.7 Longtermism provides an argument in support of the preferences of certain people. It makes it salonfähig to not just care more about innovation and economic growth than about suffering and poverty in the less developed world, but to even say that the latter is irrelevant. Longtermism is the pseudo-sophisticated support for the ideology of “tech bros” and their fanboys.8
It is for this reason that exposing the fallacies of longtermism won’t matter. It’s too easy to come up with convoluted excuses to apparently explain away those fallacies and to keep believing that there is a rational argument for what they already believed in. And that – I expect – is what longtermists will do if they cannot ignore a counterargument. In the end, longtermism is not science or philosophy, but ideology.
Closing remarks
Longtermism is an ideology founded on cluelessness about cluelessness. To support their views, longtermists pretend that they can predict the future. Reality is, of course, that we cannot. If it is taken into account that we are actually clueless about the far future (and to a far lesser extent also about the nearer future), the argument in favor of longtermism falls apart. Rather than basing our decisions about what to do upon predictions about the far future, we should do whatever we can reasonably expect to produce the best results, but such reasonable expectations are always on relatively short time scales (because, again, we are utterly clueless about the more distant future). It is the near (and mid) future that matters. The far future will have to take care of itself.
If you found this article and/or other articles in this blog useful or valuable, please consider making a small financial contribution to support this blog, 𝐹=𝑚𝑎, and its author. You can find 𝐹=𝑚𝑎’s Patreon page here.
Notes
- James Lenman (2000), “Consequentialism and Cluelessness”, Philosophy & Public Affairs 29.4: 342–70.
- In the first part of Chapter 12 of my last book, I discuss some of the most fundamental metaphysical problems. See: Lajos Brons (2022), A Buddha Land in This World: Philosophy, Utopia, and Radical Buddhism (Earth: punctum).
- See some of the other sections of the same chapter in the same book.
- Whether classical utilitarians where actually objective consequentialists is quite debatable. See the section “Consequences in Consequentialism” in the same chapter in the same book.
- The terms “subjective consequentialism” and “objective consequentialism” were introduced in: Peter Railton (1984), “Alienation, Consequentialism, and the Demands of Morality”, Philosophy & Public Affairs 13.2: 134–71.
- These are totals of absolute values to prevent relevant negative utility canceling out relevant positive utility.
- As the disposables are mostly brown or black and poor, while the people whose activities are favored by longtermists are mostly rich white men, longtermism turns out to be racist, classist, and sexist in practice.
- Yes, they’re mostly men.